Anforderungen an die Lichtverteilung

Für folgende Betrachtungen wird vereinfachend davon ausgegangen, daß eine konstante Beleuchtungsstärke über einen möglichst weiten Bereich erzielt werden soll.

Randbemerkung: Historisch bedingt sind hier teilweise noch $\alpha$ und $\beta$ gegenüber der allgemeinen Verwendung bei Scheinwerfern vertauscht. Ebenso ist die Laufrichtung noch nicht angepaßt. Dies wird bei nach und nach geändert.

Bild 3.144: Geometriedefinitionen

Aus den geometrischen Randbedingungen und Formel (3.8) ergibt sich dann Formel 3.124. Dabei wird nicht diskutiert, ob nach TA23 der Scheinwerfer feststeht und die Meßebene eine ebene Fläche ist (m.E. Wortlaut der TA23) oder der Sensor feststeht, der Scheinwerfer verschwenkt wird und die Meßfläche dadurch zu einer Kugelfläche mutiert (meines Wissens nach beim LTI angewendet).

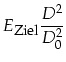$$E = E_{\mbox{\footnotesize Ziel}}\frac{D^2}{D_0^2}$$ (3.116)

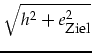$$D_0 = \sqrt{h^2+e_{\mbox{\footnotesize Ziel}}^2}$$ (3.117)

$$D = \sqrt{b^2+h^2+e^2}$$ (3.118)

$$e = h \tan(\beta_0-\beta)$$ (3.119)

$$b = \sqrt{e^2+h^2}\tan \alpha$$ (3.120)

$$\beta_0 = \arctan\frac{e_{\mbox{\footnotesize Ziel}}}{h}$$ (3.121)

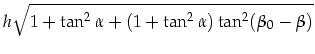$$D = h\sqrt{1+\tan^2\alpha+(1+\tan^2\alpha)\tan^2(\beta_0-\beta)}$$ (3.122)

Folglich ist

$$E=E_{\mbox{\footnotesize Ziel}}\frac{(1+\tan^2\alpha)(1+\tan... ...playstyle e_{\mbox{\footnotesize Ziel}}^2}{\displaystyle h^2}}$$ (3.123)

und damit kann Bild 3.145 generiert werden.

Bild 3.145: Korrekturfaktor für $E$ um eine gleichmäßige Fahrbahnausleuchtung zu erreichen

Wenn nur der Schnitt bei $\alpha=0$ genommen wird, dann kann Gl. 3.124 vereinfacht werden:

$$E=E_{\mbox{\footnotesize Ziel}}\frac{1+\tan^2(\arctan\frac{e... ...playstyle e_{\mbox{\footnotesize Ziel}}^2}{\displaystyle h^2}}$$ (3.124)

Diese Formel wird häufig für ,,Höhenschnitte`` verwendet.

Die Winkelabhängigkeit der Reflexion und der Retroreflexion auf der Straßenoberfläche wird vorerst nicht betrachtet, da sieht es bei regennasser Fahrbahn schlecht für den Fahrer aus (vgl. Seite ff.). Es kann davon ausgegangen werden, daß sich die Lichtaustrittshöhe $h$ der Fahrradscheinwerfer an klassischen Sicherheitsrädern^3.224 in ca. 70cm Höhe und an Liege- und Falträdern in ca. 40-50cm Höhe befindet. Aus den gesetzlichen Vorgaben (HV in 5m Entfernung in $0,5\,h$) ergibt sich bei Sicherheitsrädern ein Neigungswinkel nach unten von 4$^{\circ}$. Die Zulassungsvoraussetzungen geben für Lichtquellen mit mehr als 42lm in 10m Entfernung im Punkt HV $E_{\mbox{\footnotesize Ziel(10 m)}}$=20lx als Mindestbeleuchtungsstärke vor. Mit den anderen Daten aus der TA23 kann man ausrechnen, daß in 4,42m$\hat{=}$-5$^{\circ}$ mehr als 10,23lx und in 7,27m$\hat{=}$-1,5$^{\circ}$ mehr als 18,92lx erzielt werden müssen. Da läge man mit konstant 20lx darüber.

Die 20lx sind vorerst angenommen. Das menschliche Auge nimmt Leuchtdichten bzw. Kontraste war. Je nach den Reflexionseigenschaften des Gegenstandes bzw. der Fahrbahn wird die Beleuchtungsstärke umgewandelt. Soll der Fahrradscheinwerfer als Scheinwerfer und nicht nur als Positionslaterne dienen, so sind für eine genaue Auslegung der erforderlichen Beleuchtungsstärke also Kenntnisse über die erforderliche Leuchtdichte und die Reflexionseigenschaften notwendig: Versuche von Dunbar[Du38] ergaben eine minimale Leuchtdichte von 2cd/m$^2$, bei der Hindernisse sicher erkannt werden können. Auch andere Untersuchungen haben diesen 1938 publizierten Wert bestätigt, so daß heute 2cd/m$^2$ allgemein für Straßen mit größerer Verkehrsbelastung gefordert werden. Da die Reflexionseigenschaften des Bodens bzw. der Straße zu unterschiedlich sind kann nicht einfach von Leuchtdichte auf Beleuchtungsstärke umgerechnet werden. Spätestens hier wird der theoretisch radikale Ansatz ein Ratespiel. Deswegen folgt ein praktisches Schielen auf die Regelungen für motorisierten Verkehrsteilnehmer.

Bei Kraftfahrtzeugen sieht die ECE-Regelung 20 für Scheinwerfer mit Ablendlicht einige Richtwerte vor[Sc92]. So werden in 50m Entfernung direkt vor dem Auto mehr als 6lx, an der rechten Straßenseite^3.225 mehr als 12lx und an der linken Straßenseite weniger als 15lx gefordert. Die Beleuchtungsstärken sind für den Meßpunkt in 25m Entfernung angegeben. Umgerechnet auf 10m ergeben sich mehr als 37,5lx vor dem Auto; auf 50m 1,5lx. In 25m Entfernung werden an beiden Straßenseiten mehr als 2lx gefordert. Das sind 12,5lx in 10m. Nach oben dürfen maximal 0,7lx abgestrahlt werden. Das sind auf 10m umgerechnet 4,4lx, mehr als das Doppelte des bei Fahrrädern akzeptierten Wertes. Diese Werte sind mit der begrenzten Leistung am Fahrrad nicht sinnvoll zu erreichen.

Laut ECE-R112 (Halogenscheinwerfer) sind in 25m Entfernung im Punkt B50L (Gegenspur, 50m Entfernung, Augenhöhe entgegenkommender Kfz-Fahrer) max. 0,4lx bzw. nach ECE-R98 (Gasentladungsscheinwerfer) max. 0,5 lx pro Scheinwerfer zulässig.

Zum Thema Blendung durch Scheinwerfer ist z.B. [Loch08] lesenswert.

Die Begrenzungen bestehen aus folgenden Randbedingungen:

1. Die Einhaltung des Grenzwertes von max. 2lx bei 89,6$^{\circ}$.

2. Die verfügbare Lichtleistung (die ausgeleuchtete Fläche ist auch vorgeschrieben).

3. Kurz vor dem Rad wird kein Licht mehr benötigt (da kann man während der Fahrt eh nicht mehr reagieren). Diese Zone wird vorerst mit 2m abgeschätzt. Continental gibt 0,9s als Zeit zwischen Erkennen des Hindernisses und vollem Bremsdruck an, in alten Führerscheinunterlagen stehen drei Sekunden.^3.226 Bei einer Geschwindigkeit von 20km/h=5,6m/s sind 2m auch für niedrigere Geschwindigkeiten ausreichend. Außerdem wird so nah am Fahrrad relativ wenig Lichtleistung benötigt.

Daraus kann das Bild 3.146 der Beleuchtungsstärkeverteilung konstruiert werden. Man beachte die logarithmische Skalierung. Die gemessenen Daten der Scheinwerfer stammen, wenn nicht anders definiert, aus der Tabelle 3.17.

Bild 3.146: Beleuchtungsstärke (gewünscht, gefordert und erreicht)

Wie der cut-off über 0$^{\circ}$ erfolgt ist sowohl Geschmacksache als auch eine Frage der zur Verfügung stehenden Leistung und am Wesentlichsten: Fähigkeiten in der Herstellung der Optik.

Diverse Leute träumen immer noch von kleinen Reflektoren in Zusammenhang mit niedriger Anbauhöhe. Damit dieser Albtraum endlich ein Ende nehme wird hier ein Bild dagereicht, das durch die Verwendung einer einfachen linearen Skalierung und auf 10lx in 10m normierte Scheinwerfer hinreichend prägnant sein dürfte. Beispiel sind einfach nur drei ausgeführte Scheinwerfer und eine dichte Reihe von Meßpunkten.^3.227

Bild 3.147: Beleuchtungsstärke, real und theoretisch erforderlich

Und je weiter man leuchten will, desto steiler muß die Höhenschichtung sein. Da hilft nur eines: Kleine lichtemittierende Fläche, große Brennweite des Reflektors und eine hohe Oberflächenqualität des Reflektors. Wer diese drei Punkte nicht beherzigt wird nie einen guten Scheinwerfer für den Fahrradbereich erhalten.

Einige weitere Anmerkungen hierzu s. S. .

Mit der bis hier entwickelten idealen Ausleuchtungscharakteristik direkt nach vorne können sicherlich alle leben. Die seitliche Ausleuchtungscharakterisitik ist nicht so klar definierbar. Eine schmale helle Keule spricht für viele Fahrten bei wechselnden Lichtverhältnissen und Nässe auf geraden schnellen Wegen. Eine breite Keule wird von Radfahrern bevorzug, die viele Kurvenfahrten haben oder z.B. auf unbefestigten Wege unterwegs sind. Breit und hell und lang geht aufgrund der beschränkten Leistung nicht, man muß sich für sein Optimum entscheiden oder z.B. einen zuschaltbaren (Serien-)Scheinwerfer als Fernlicht verwenden.

Für die Straßenbeleuchtung gibt die DIN 5044 Teil 2 einen üblichen Leuchtdichtekoeffizient von 0,05-0,13cd/(m$^2\cdot$lx) an. Dies gilt bei einem Betrachtungswinkel von ca. 0,5-1,5$^{\circ}$.^3.228 Bei der Beleuchtung durch den eigenen Fahrradscheinwerfer ist aufgrund des stark schräg aufkommenden Lichtes eher mit dem unteren Grenzwert, bei Nässe mit noch weniger, zu rechnen. Damit bleiben bei 20lx ca. 1cd/m$^2$ übrig. Dieser Wert liegt an der unteren Grenze zur Dunkeladaption (vgl. S. ). Bei Nässe wiederum wird das Licht entgegenkommender Kraftfahrzeuge nur schwach gestreut und fast direkt reflektiert. Mit diesen Leuchtdichteunterschieden wird die Fahrradfahrt dann meist zum Blindflug.

Auf Reflexionsflächen ist, soweit möglich, zu verzichten, da der Reflexionsgrad $b$ kaum über den 92% für hochglanzpoliertes Silber liegen wird.^3.229 Hochglanzpoliertes Aluminium wird mit 80-87% angegeben. Bei einem typischen Fahrradscheinwerfer werden ca. $a=75\,$% des Lichtstromes reflektiert^3.230 und der gesamte Lichtstrom noch durch die Frontscheibe (Transmissionsgrad ca. $c=87\,$%) reduziert.^3.231

Dann bleiben von der Nennlichtausbeute ( $\eta_{\mbox{\footnotesize HS3}}=15$lm/W) nur noch

$$\eta_{\mbox{\footnotesize real}}=\eta(1+a(b-1))=15\mbox{ lm/... ...0,87(1+0,67(0,87-1))=15\mbox{ lm/W}\cdot 0,79=11,9\mbox{ lm/W}$$ (3.125)

übrig. Die Frontscheibe ist meist als Fresnel-Linse ausgebildet und kann nur auf eine Lichteinfallrichtung optimiert werden: Entweder vom Reflektor kommendes oder von der Lampe kommendes Licht. Da bei normalen Scheinwerfern ein Großteil des Lichts reflektiert wird (vgl. S. ff.), wird die Linse vorwiegend auf dahingehend ausgelegt, daß das reflektierte Licht optimal gerichtet wird. Daß heißt wiederum, daß bei normalen Scheinwerfern ca. 30% des Lichtstromes außerhalb des zentralen Lichtkegels ,,verschwendet`` werden. Dies erhöht in erster Milchmädchenrechnung zwar die seitliche Ausleuchtung. Aber sobald man sich die Leuchtdichteunterschiede und die auszuleuchtenden Flächen vorstellt, geht diese Rechnung nicht mehr auf: Diese Lichtmenge ist als verloren zu betrachten!

Daraus folgt, daß bei symmetrischen Scheinwerfern mit durchschnittlicher Rücklage der Lampe fast der gesamte nutzbare Lichtstrom reflektiert wird. Damit sinkt die Lichtausbeute auf

$$\eta_{\mbox{\footnotesize real}}=15\,\mbox{ lm/W}\cdot 0,7\cdot 0,87\cdot 0,87=7,9\,\mbox{ lm/W}$$ (3.126)

Damit kann man sich wirklich schon im Jahre 2000 ernsthafte Gedanken um die Verwendung weißer LEDs machen.

Weiterhin verschwenden stark rückspringende Scheinwerfer mit einer Frontscheibe, die nicht als Fresnel-Linse ausgebildet ist, z.B. der Hella FF-Tech, viel Licht nutzlos nach oben.