Nächste Seite: Messungen an Rückleuchten Aufwärts: Optimaler Scheinwerfer Vorherige Seite: Anforderungen an die Lichtverteilung Inhalt Index
An anderen Stellen wurde schon angerissen, daß die Grenze der seitlichen Ausleuchtung ein Streitpunkt ist.
Damit ergeben sich auf der Fahrbahn die in Bild 3.148 abgebildete Projektionen.
Scheinwerfer werden i.a. in einer Wandprojektion vermessen (vgl. Punkt 1) und konstruiert. Für diese muß die Straßenprojektion umgerechnet werden. Die Grenzen der Ausleuchtungswinkel lassen sich analytisch berechnen bzw. sind definiert:
Für den Fall 1: Siehe Seite ![[*]](crossref.png) ff.
ff.
Für den Fall 2:
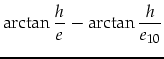 |
(3.127) | ||
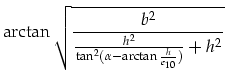 |
(3.128) | ||
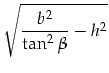 |
(3.129) |
Für den Fall 3:
| (3.130) | |||
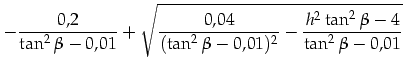 |
(3.131) | ||
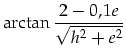 |
(3.132) |
Damit ergibt sich mit ![]() m Bild 3.149 abgebildet.
m Bild 3.149 abgebildet.
Zusätzlich ist die Entfernung ![]() vor dem Scheinwerfer in Abhängigkeit von
vor dem Scheinwerfer in Abhängigkeit von
![]() (für
(für ![]() ) bzw.
) bzw. ![]() (für Fall 2 und 3) mit angegeben.
Bitte die logarithmische-Skala für
(für Fall 2 und 3) mit angegeben.
Bitte die logarithmische-Skala für ![]() beachten.3.232
beachten.3.232
Rechnet man für diese Ausleuchtungsbilder den erforderlichen Lichtstrom aus
und bezieht ihn auf 1lx und 1m![]() ausgeleuchteten Boden, so ergibt sich
Bild 3.150. Hierbei wird in den Schritten im Bereich
+-0,5m gerechnet.
ausgeleuchteten Boden, so ergibt sich
Bild 3.150. Hierbei wird in den Schritten im Bereich
+-0,5m gerechnet.
Gleichung 3.134 enthält ein Korrekturfaktor für die
Entfernungsverhältnisse und die schräge Einstrahlung. In den Grenzen
![]() und
und ![]() des gewünschten Leuchtfeldes muß diese integriert
werden um den Lichtstrom zu erhalten.
des gewünschten Leuchtfeldes muß diese integriert
werden um den Lichtstrom zu erhalten.
Damit kann man dann ungefähr abschätzen, wie groß der Lichtstrom sein
muß, den man für gewünschte Ausleuchtungsfelder benötigt. Randbemerkung:
Natürlich wird allerdings nahe am Rad bei großem ![]() der Lichtstrom
ansteigen.
der Lichtstrom
ansteigen.
Rein theoretisch würden für 1lx auf 1m![]() wiederum 1lm reichen (vgl.
S. 3.7).3.233
wiederum 1lm reichen (vgl.
S. 3.7).3.233
Olaf Schultz, Hamburg-Harburg