Theoretische Vorüberlegungen zum LED-Scheinwerfer

Was für eine Strahlstärke und Strahlstärkenverteilung müßte eine LED aufweisen, um die erforderlichen Lichtwerte zu erzeugen?

$$I=E_{\mbox{\footnotesize TA24}}r^2$$ (3.59)

Für eine HS4 ergeben sich damit 2000cd. Für die horizontale Ebene muß der Sichtwinkel $2\Phi_{1/2}$ größer als 8$^{\circ}$ sein. Vertikal dürfen oberhalb von 3,4$^{\circ}$ maximal 200cd abgestrahlt werden, während unterhalb bei 5$^{\circ}$ zu jeder Seite mindestens 100cd gefordert sind. Dies erfordert eine stark angepaßte Auslegung der Abstrahlcharakteristik. Von Nichia gibt es schon LEDs mit einer ovalen Ausleuchtungsform, aber noch nicht in der hier geforderten Form. Für die genaue Bestimmung der Mindest-/ Maximalstärken ist die TA 23 (siehe Anhang, S. ) heranzuziehen.

Da derzeit^3.62 so starke LEDs noch nicht erhältlich sind müßten andere Wege beschritten werden. Nur mal so, als abschreckendes Rechenbeispiel für diejenigen, die immer noch einem LED-Scheinwerfer hinterherhecheln: Nehmen wir mal an, eine weiße LED habe als Spitzenwert 5,6cd und dabei einen Spannungsabfall von $U=3,6$V@$I=20$mA mit Stückkosten von 2DM/Stk. Wieviele $n$ LEDs braucht man, um zumindest in HV $E_{\mbox{\footnotesize TA24}}$ zu erzeugen? Als Randbemerkung: Das Formelzeichen $I$ wird hier sowohl für den Strom, Einheit A, wie für die Lichtstärke, Einheit cd, verwendet, bitte nicht durcheinanderbringen.

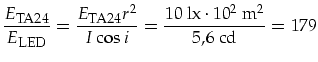$$n = \frac{E_{\mbox{\footnotesize TA24}}}{E_{\mbox{\footnotesize LED}}... ...24}} r^2}{I \cos i}=\frac{10\mbox{ lx}\cdot 10^2\mbox{ m}^2}{5,6\mbox{ cd}}=179$$ (3.60)

Den einstrahlenden Winkel legt die TA 23 (2) mit 0 Grad fest,^3.63 $\cos i$ ist folglich 1.

Mit 179 LEDs kostet der Scheinwerfer alleine an LEDs, je nach Händler, ca. 360DM. Allerdings ohne Mehrwertsteuer, Arbeitskosten, Platine, Steuerung etc. Dabei verbraucht er dann auch noch mit

$$P=n U I=179\cdot 3,6\mbox{ V}\cdot 0,02\mbox{ A}=12,9\mbox{ W}$$ (3.61)

eine derzeit^3.64 unakzeptable Leistung. Diese beiden Preise sind wohl ein bißchen hoch für eine allerdings wahrscheinlich hohe Zuverlässigkeit. Auch bei LEDs gibt es zum Glück einen Fortschritt, also abwarten.

Und nun anders rum. Um die Stromwerte und elektrischen Leistungswerte einer HS3 zu erfüllen ist nur eine maximale Anzahl $n$ von LEDs zulässig. Rechnen wir mal mit 20mA/LED, bis auf einige Exoten, wie die Luxeon Star's, der Durchschnitt, so ergibt sich:

$$n=\frac{P_{\mbox{\footnotesize HS3}}}{P_{\mbox{\footnotesize LED}}}=\frac{2,4\mbox{ W}}{3,6\mbox{ V}\cdot 0,02\mbox{ A}}=33$$ (3.62)

Bei 33 LEDs ist aber noch keine Sicherheitsreserve für die notwendige Stromregelung vorgesehen. Rechnen wir sicherheitshalber mal mit 30 LEDs weiter.

Noch eine Randbemerkung: Das Maximum des spektrale Helligkeitsempfindens des menschlichen Auges ist von den Lichtverhältnissen abhängig:

• Das helladaptierte Auge hat seine größte Empfindlichkeit bei ca. 555nm (Übergang Gelb-Grün). Hier haben die farbsensitiven Zäpfchen ihr Empfindlichkeitsmaximum. Ein Grund dafür ist in der Evolution zu finden: Unsere hellste natürliche Lampe, die Sonne, hat bei ca. 555nm ihr Intensitätsmaximum.

• Das dunkeladaptierte Auge hat seine größte Empfindlichkeit bei ca. 507nm (Übergang blau-grün). Ein Grund dafür ist wiederum in der Evolution zu finden: Hat schon mal jemand, außer bei Polarlichtern, Bränden o.ä. nachts einen roten Himmel gesehen? Bei 507nm haben die Stäbchen ihr Empfindlichkeitsmaximum. Farben können nicht mehr erkannt werden (Nachts sind alle Katzen grau).

Der Übergang vom Zäpfchen- zum Stäbchensehen tritt laut [DTVLex] bei ca. $10^{-6}\ldots10^{-3}$sb, entspricht 0,1...100cd/m$^2$, auf. Nach [HeMa] findet der Übergang bei ca. 0,001cd/m$^2$ statt. Die Zapfen adaptieren sich relativ schnell innerhalb von fünf Minuten auf 10$^{-3}$cd/m$^2$, die Stäbchen haben sich nach ca. 20Minuten weitgehend adaptiert. Mit einer verringerten Leuchtdichte geht eine vergrößerte Reaktionszeit einher. Hierzu gibt es mehrere Untersuchungen, z.B. [Bu99], auf die hier nicht weiter eingegangen wird.

Bild 3.34: Spektraler Helligkeitsempfindlichkeitsgrad für photometrische Normalbeobachter nach CIE

Dunkeladaptiert ist eine rote LED bei gleicher Strahlstärke visuell dunkler als eine in blau oder grün. Unter anderem könnten deswegen die Xenon-Gasentladungslampen mit ihrem betont blauen Anteil nachts heller erscheinen als die eher rötlicheren Halogenlampen. Hier greifen auch die ,,modernen`` blue vision-Lampen ein. Dazu werden ausgesucht helle Halogenlampen genommen und mit einem bläulichem Lack überzogen. Die rötlichen Anteile, auf die das dunkeladaptierte Auge unempfindlicher ist, werden herausgefiltert. Da aber Radfahrer in der Regel nicht dunkeladaptieren können, die Lichtverschmutzung durch Auto- und Straßenbeleuchtung verhindert dies, dürften doch wahrnehmbar Lichtanteile fehlen. Solche Lampen werden teilweise als ,,Xenon-Licht`` beworben und wollen dadurch auf die Xenon-Gasentladungslampen zielen, sind aber nur mit Xenon gefüllte Glühfadenlampen. In diesem Zusammenhang: Ein vollständige Dunkeladaption ist erst nach ca. 40Minuten erreicht,^3.65 ist aber in wenigen Sekunden rückgängig gemacht. Spezielle Adaptionsbrillen, die aus einem zwischen 640-680nm durchlässigem Rotfilter bestehen, erhalten die Dunkeladaption [DTVLex].