Nächste Seite: UK1 Aufwärts: Fahrradbeleuchtung Vorherige Seite: SONquelle Inhalt Index
Für die Charakterisierung der Kugeln können folgende Kenndaten verwendet
werden. Die gesamte Kugelinnenfläche ![]() setzt sich aus der Kugelfläche und
der Fläche des Schatters zusammen. Die Störflächen
setzt sich aus der Kugelfläche und
der Fläche des Schatters zusammen. Die Störflächen
![]() setzen sich aus der
des Sensorfensters, des Eintrittsfenster und des Trennspaltes zusammen. Das
Verhältnis (
setzen sich aus der
des Sensorfensters, des Eintrittsfenster und des Trennspaltes zusammen. Das
Verhältnis (![]() ) zwischen Störflächen und Gesamtfläche sollte unter 5%
liegen.
) zwischen Störflächen und Gesamtfläche sollte unter 5%
liegen.
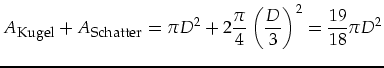 |
(G.1) | ||
| (G.2) | |||
| (G.3) | |||
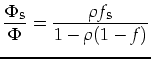 |
(G.4) | ||
| (G.5) |
mit dem Kugeldurchmesser ![]() , der Trennspaltdicke
, der Trennspaltdicke ![]() , dem Durchmesser des
Sensorfensters
, dem Durchmesser des
Sensorfensters
![]() , dem Durchmesser des Eintrittsfensters
, dem Durchmesser des Eintrittsfensters
![]() und dem DurchgangG.1
und dem DurchgangG.1 ![]() . Die Reflektivität
. Die Reflektivität ![]() der Beschichtung wird aus Formel
(3.9) berechnet.
der Beschichtung wird aus Formel
(3.9) berechnet.