Hydraulikbremsen

Vorerst sind hier nur Geometriedaten aufgeführt. Sinn ist es, daß nicht andere, wie ich, z.B. auf den kleinen Lenkerrohrdurchmesser der Sachs reinfallen.

Der Kolbendurchmesser ist $d_{\mbox{\footnotesize KG}}$, der Lenkerrohrdurchmesser $d_l$, der Abstand zwischen Drehpunkt und Zylinderachse $l_1$, der Abstand zwischen Drehpunkt und Hand-Angriffspunkt $l_2$ (Ich habe hier den Spalt zwischen Mittel- und Ringfinger und gewählt) und die Masse $m$ (ungefüllt/gefüllt).

Tabelle 7: Daten von Hydraulikbremsgebern

Modell	$d_{\mbox{\footnotesize KG}}$	$l_1$	$l_2$	$d_l$	$m$
Magura (alt)	18,0	15	80	22-24	90/
Magura Renn	16,0	15	80	22-24	117/
Magura HS22	16,0	14	70	22	/160
Magura Raceline D	14,0
Sachs Powerdisc	12,5	17	75	22,x	118/

Magura alt heißt hier ,,Magura Hydro Stop``: Niroschelle, Alukörper, bis ca. '94 gebaut.¹²⁹

Die Daten der Nehmersysteme sind in der Tabelle 8 wiedergeben. Die Anzahl der Nehmersysteme (Kolben) ist $z$.

Tabelle 8: Daten von Hydraulikbremsnehmern

Modell	$d_{\mbox{\footnotesize KN}}$	$z$	$m$
Magura (Alukolben)	14	2
Magura (PA-Kolben)	14	2
Magura Renn		1
Sachs Powerdisc	20	1

Hieraus kann dann die Kraftübersetzung $i$ der Bremse berechnet werden:

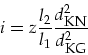$$i=z\frac{l_2}{l_1}\frac{d^2_{\mbox{\footnotesize KN}}}{d^2_{\mbox{\footnotesize KG}}}$$ (1)

Die Kraftübersetzung $i$ beträgt bei Magura ca. 17,6. Die gilt nicht für die Magura Rennbremse, da diese noch in der Bremszange eine Hebelübersetzung aufweist.

Die verzögerungswirksame Bremskraft $F_{\mbox{\footnotesize Brems eff.}}$ berechnet sich aus der Kraft der Bremsklötze auf der Felge $F_{\mbox{\footnotesize Brems}}$ und dem Reibbeiwert $\mu$ sowie dem Hebelarmverhältnis der Kraftangriffe. Die Bremsverzögerung $a$ ist wiederum aus der Gesamtmasse von Fahrrad, Gepäck und Fahrer $m_{\mbox{\footnotesize gesamt}}$ sowie der effektiven Bremskraft $F_{\mbox{\footnotesize Brems eff.}}$ berechenbar.¹³⁰

$$F_{\mbox{\footnotesize Brems}} = i F_{\mbox{\footnotesize Hand}}$$ (2)

$$F_{\mbox{\footnotesize Brems eff.}} = \mu \frac{d_{\mbox{\footnotesize Bremsscheibe eff.}}}{d_{\mbox{\footnotesize Laufrad}}} F_{\mbox{\footnotesize Brems}}$$ (3)

$$a = \frac{F_{\mbox{\footnotesize Brems eff.}}}{m_{\mbox{\footnotesize gesamt}}}$$ (4)

Der effektive Bremsscheibendurchmesser $d_{\mbox{\footnotesize Bremsscheibe eff.}}$ ist z.B. bei einer Felgenbremse ungefähr der ETRTO-Durchmesser. Bei der Sachs Neos-Scheibe (Stahl) beträgt $d_{\mbox{\footnotesize Bremsscheibe eff.}}=130$ mm.

Last but not least in diesem Abschnitt ein paar Worte zum Hydrauliköl. Man kann laut Magura zum (Nach-) Füllen sowohl Nähmaschinenöl als auch LHM+ (diese schön giftgrüne Soße von Citroën) verwenden. Nach unseren Messungen mit einem Rheometer (Platte-Kegel) sollte Nähmaschinenöl mit 2,5 cSt@100 $^{\circ}$C) im interessanten Temperaturbereich dünnflüssiger sein als das LHM+ mit 5 cst@100 $^{\circ}$C. Mit extrapolierten 110 cSt@-25 $^{\circ}$C sollten Nähmaschinenöl und LHM+ gleich hochviskos sein. Trotz diesem Vorteil von Nähmaschinenöl bin ich aufgrund der relativen Temperaturempfindlichkeit auf LHM+ umgestiegen. Und von dem einem Liter für ca. 35 DM sind nach 5 Jahren immer noch 0,5 Liter über. Der Rest waren Planschverluste (Schiet, das Glas war schon wieder nicht zugeschraubt).