28'' SON

Hier wird ein 1997 gekaufter SON, alte Bauform, mit Scheibenbremsaufnahme getestet. Ein besonderes Augenmerk wird auf den Wirkungsgrad und die Übereinstimmung mit Wullkopf gelegt (siehe hierzu auch Bild 2.22). Der Dynamo wird mit dem Nabengehäuse in einer Drehbank eingespannt, die Achse mit einem Hebel ($l=140$mm) versehen.

Als Lastwiderstände werden $R_{\mbox{\footnotesize a}}$=47/15W und $R_{\mbox{\footnotesize a}}$=25/10W (Alugehäuse, gekühlt) verwendet.

Tabelle 2.28: Meßwerte 28''-SON (Drehbank)

$v$	n	$R_{\mbox{\footnotesize a}}=10\,\mbox{M}\Omega$		$R_{\mbox{\footnotesize a}}=25\,\Omega$		$R_{\mbox{\footnotesize a}}=47\,\Omega$
[km/h]	[1/min]	$U_0$	$P_{\mbox{\footnotesize m}}$	$U$	$\eta$	$U$	$\eta$
11,2	87	-	-	-	-	6,8	38,72
16,2	125	12	-	8,9	53,41	10,6	57,95
25,9	200	18,6	1,21	11,9	52,51	15,4	54,82
40,7	315	30,1	2,81	14,2	54,28	21,5	59,26
64,7	500	48,1	9,06	15,5	46,4	26,4	58,21
103,4	800	75	20,7	16,6	37,72	30,3	51,59
161,6	1250	106	43,1	17,1	30,94	31,7	44,59

Dies sind die ersten Messungen auf der Drehbank. Spätere Messungen werden leicht abgewandelt, besonders in der Wahl der Lastwiderstände.

Das Bild 2.22 zeigt die Abhängigkeit der Leistung von der Geschwindigkeit vom SON.

Bild 2.22: Leistungsmessung 28''-SON

Als Strom $I_{\infty}$ wird in Bild 2.22 mit 0,7A gerechnet.

Als zweiter 28''-SON wird einer von Schmidt aus der 1999er Produktion verwendet. Dieser wird mit der auf Seite eingeführten Zusatzmasse $J_{\mbox{\footnotesize z}}$ getestet! Dieser Dynamo hat $R_{\mbox{\footnotesize i}}=2,79\,\Omega$, $L_{\mbox{\footnotesize i}}=0,037-0,06$H, $R_s=72-173\,\Omega$.

3pt

Tabelle 2.29: Meßwerte 28''-SON (zweiter, mit $J_{\mbox{\footnotesize z}}$)

$v$	n	$R_{\mbox{\footnotesize a}}=10\,\mbox{M}\Omega$		$R_{\mbox{\footnotesize a}}=0,1\,\Omega$		$R_{\mbox{\footnotesize a}}=12\,\Omega$		$R_{\mbox{\footnotesize a}}=24\,\Omega$
[km/h]	[1/min]	$U$	$P_{\mbox{\footnotesize m}}$	$I$	$P_{\mbox{\footnotesize m}}$	$U$	$\eta$	$U$	$\eta$
6,2	48	4,55	0,12	0,34	1,32	3,25	61,64	3,87	60,8
10,3	80	6,27	0,21	0,54	1,65	4,65	57,68	5,95	60,1
16,2	125	12,2	0,46	0,57	2,14	5,85	59,85	8,9	69,27
20,7	160	15,0	0,89	0,58	2,68	6,3	55,59	10,1	66,45
25,9	200	18,9	1,3	0,59	3,72	6,58	51,06	11,3	65,03
51,7	400	38,16	3,72	0,61	6,47	7,18	41,26	13,56	56,29
64,7	500	49,7	5,58	0,61	8,37	7,36	35,18	14,06	50,63
103,4	800	80,8	12,2	0,62	13,39	7,4	25,56	14,47	41,89
206,9	1600	160,3	37,78	0,65	30,35	7,78	15,14	15,41	25,58
323,3	2500	246,5	92,97	0,66	43,23	7,86	9,23	15,62	16,2

$v$	$R_{\mbox{\footnotesize a}}=29,4\,\Omega$		$R_{\mbox{\footnotesize a}}=88\,\Omega$		$R_{\mbox{\footnotesize a}}=110\,\Omega$		$R_{\mbox{\footnotesize a}}=132\,\Omega$
[km/h]	$U$	$\eta$	$U$	$\eta$	$U$	$\eta$	$U$	$\eta$
6,2	3,95	66,07	-	-	-	-	-	-
10,3	6,30	64,82	-	-	-	-	-	-
16,2	9,55	70,25	-	-	-	-	-	-
20,7	11,10	64,62	-	-	-	-	-	-
25,9	14,74	86,40	-	-	-	-	-	-
51,7	16,12	59,12	-	-	-	-	-	-
64,7	16,87	53,40	-	-	-	-	-	-
103,4	17,44	40,43	-	-	-	-	-	-
206,9	18,68	28,50	53,7	52,7	64,1	55,6	74,7	57,9
323,3	19,07	21,46	-	-	-	-	-	-

Randbemerkung: Der durch $\approx$160V verursachte Strom zwiebelt ganz gut, selbst wenn er nur durch die Finger einer Hand fließt!^2.45

Und mal, rein Interessehalber, Wullkopf rückwärts:

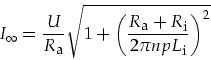$$I_{\infty}=\frac{U}{R_{\mbox{\footnotesize a}}}\sqrt{1+\left... ...otnotesize i}}}{2\pi n p L_{\mbox{\footnotesize i}}}\right)^2}$$ (2.31)

Bei 1600 min$^{-1}$ ergeben sich mit den Werten bei $R_{\mbox{\footnotesize a}}=$132, 88, 24 und 12 $I_{\infty}$=0,58, 0,61, 0,64 und 0,65 A.

Der Dynamo aus der Tabelle 2.28 ergeben auf dem MufuZ die Meßwerte in der Tabelle 2.30

Tabelle 2.30: Meßwerte 28'' SON (eingefahren)

n	v	$R_{\mbox{\footnotesize a}}=0,8\,\mbox{M}\Omega$		$R_{\mbox{\footnotesize a}}=0,1\,\Omega$		$R_{\mbox{\footnotesize a}}=12\,\Omega$		$R_{\mbox{\footnotesize a}}=24\,\Omega$
[1/min]	[km/h]	$U$	$P_{\mbox{\footnotesize m}}$	$I$	$P_{\mbox{\footnotesize m}}$	$U$	$\eta$	$U$	$\eta$
80	10	9,5	0,52	0,62	1,6	5,14	65,99	6,91	72,53
100	12,5	-	-	-	-	5,66	64,01	7,81	66,89
120	15	13,95	0,89	0,63	2,22	6,17	62,01	9,17	68,49
159	20	18,21	1,84	0,65	3,17	6,75	58,2	10,74	64,83
239	30	26,8	3,38	0,65	5,34	7,23	50,74	12,7	60,43
319	40	34,68	5,34	0,66	5,93	7,45	43,32	13,49	55,58
478	60	50,30	10,23	0,68	11,57	7,77	37,7	14,55	49,57

Die Geschwindigkeit ist mit einem Laufradumfang von 2090mm gerechnet.