Bestimmung der verschiedenen Konstanten

Um die in Gl. (T.10) vorkommenden Konstanten zu erhalten, ist es notwendig, mit dem betreffenden Dynamosystem die Funktion $U(v)$ möglichst genau aufzunehmen. Dazu muß die vom Dynamo abgegebene Spannung $U$ am Widerstand $R_{\mbox{\footnotesize a}}$ bei verschiedenen Geschwindigkeiten $v$ gemessen werden. Dann sind der ohmsche Widerstand der Wicklung $R_{\mbox{\footnotesize i}}$ zu messen und die Windungszahl $w$ zu bestimmen. Ist $p$ die Polpaarzahl des Läufers und $d$ der Durchmesser des Antriebsrädchens, so ergibt sich $A$ aus Gl. (T.4); aus Gl. (T.12) erhält man $b$ zu:

$$b=\left(\frac{\mbox{d} U}{\mbox{d} v}\right)_{v=0} \frac{R_{... ...}+R_{\mbox{\footnotesize i}}}{A w R_{\mbox{\footnotesize a}}}$$ (T.13)

wobei das erste Glied auf der rechten Seite von Gl. (T.13) die Steilheit der Kurve $U(v)$ an der Stelle $v=0$ ist und in Vh/km gemessen wird.

Aus Gl. (T.10) ergibt sich für $l_2$, wobei $l$ zweckmäßig in Vh/A anzusetzen ist, die Beziehung:

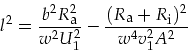$$l^2=\frac{b^2 R_{\mbox{\footnotesize a}}^2}{w^2 U_1^2}-\frac... ...footnotesize a}}+R_{\mbox{\footnotesize i}})^2}{w^4 v_1^2 A^2}$$ (T.14)

wobei die Werte von $A$, $b$, $w$, $R_{\mbox{\footnotesize a}}$, $R_{\mbox{\footnotesize i}}$ wie vorher angegeben, anzusetzen sind und $U_1$, die bei einer bestimmten Geschwindigkeit $v_1$ gemessene Spannung am Widerstand $R_{\mbox{\footnotesize a}}$ ist. Nunmehr sind alle Kenngrößen von Gl. (T.10) bestimmt, und $U=f(v)$ nach dieser Beziehung muß mit der aus der Messung sich ergebenden Kennlinie möglichst gut übereinstimmen. Aus Gl. (T.10), (T.11) und (T.12) ist der Einfluß der verschiedenen Größen auf die Kennlinie des Dynamos zu erkennen. Durch Veränderung einzelner dieser Größen gemäß vorherigem Abschnitt lassen sich unter Umständen die Eigenschaften des Dynamos erheblich verbessern.

Tabelle T.1: Kenngrößen von Fahrraddynamos

1	2
Kenngröße	Maßeinheit
$w$	-
$R_{\mbox{\footnotesize i}}$
$p$	-
$d$	mm
$A$	km$^{-1}$
$\left(\frac{\mbox{d} U}{\mbox{d} v}\right)_{v=0}$	Vhkm$^{-1}$
$b$	Vh
$U(v=30$km/h)	V
$l^2$	(VhA$^{-1}$)$^2$
$\lim_{v\rightarrow\infty} U$	V
$R_{\mbox{\footnotesize a}}$