Nächste Seite: Einfluß auf die Messung Aufwärts: Trägheitseinfluß Vorherige Seite: Berechnung aus der Pendelzeit Inhalt Index
Ein neuerer, zerlegter lightSPIN weist folgende, hier interessante, Bauteile auf:
Alle zusammen ergeben ein ![]() . Die leichten, dünnwandigen, eher achsnahen
Kunststoffteile werden vernachlässigt! Der äußere Rückschluß berechnet
sich als:
. Die leichten, dünnwandigen, eher achsnahen
Kunststoffteile werden vernachlässigt! Der äußere Rückschluß berechnet
sich als:
| (I.8) | |||
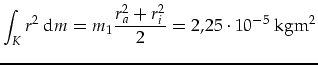 |
(I.9) | ||
| (I.10) | |||
| (I.11) |
Der innere Kreis wird als dickwandiges Rohr vereinfacht:
| (I.12) | |||
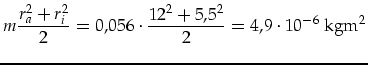 |
(I.13) |
Die gemessene Gesamtmasse des Läufers liegt bei 146g, die der berechneten
Metallteile bei 128g. Der Unterschied liegt mit 13% augenscheinlich hoch,
allerdings ist die Differenz eher achsnah, also mit einem geringen Beitrag
zum Trägheitsmoment, angeordnet. Damit ergibt sich ein ![]() von
von
| (I.14) |
Dies ist zwar größer als der aus dem Auspendel berechnete Wert; für eine grobe Abschätzung reichen diese Werte aber.
Olaf Schultz, Hamburg-Harburg