Rechnerische Abschätzung der Eigenfrequenz

Betrachtet man jetzt das Eigenschwingungsverhalten, so sind es in der Regel, durch Vertikalbeschleunigungen verursachte Biegeschwingungen. Dabei können sich die Windungen berühren und verschweißen. Kritisch dürfte für die Abschätzung die erste Eigenform sein. Als erster Ansatz dürfte der eines langen Biegestabes zulässig sein. Hier wird der Ansatz aus [HoDr], S. 290 ff. verwendet:

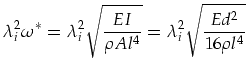$$\omega_i = \lambda_i^2\omega^*=\lambda_i^2\sqrt{\frac{EI}{\rho A l^4}}=\lambda_i^2\sqrt{\frac{Ed^2}{16\rho l^4}}$$ (3.43)

$$\lambda_i^2 = i^2 \pi^2 \qquad\mbox{bei gelenkiger Lagerung}$$ (3.44)

$$\lambda_i^2 = (i+0,5)^2 \pi^2 \qquad\mbox{bei beidseitig starrer Einspannung}$$ (3.45)

Hierbei sind $\omega^*$ die Bezugskreisfrequenz und $\omega_i$ die $i$-ten Eigenfrequenzen. Hiermit ergeben sich für die OSRAM-Lampe folgende Frequenzen:

$$\omega^* = \sqrt{\frac{305\mbox{ GPa}\cdot 0,04^2\mbox{ mm}^2\mbox{ dm}^3}{16\cdot 19,27\mbox{ kg}\cdot 13,4^4\mbox{ mm}^4}}=222\mbox{ s}^{-1}$$

$$f_1 = \frac{\omega_1}{2\pi}=\frac{222\cdot 1,5^2\cdot \pi^2}{2\pi}=\mbox{785\,Hz}$$

$$f_2 = \frac{222\cdot 2,5^2\cdot \pi^2}{2\pi}=\mbox{2179\,Hz}$$

$$f_3 = \frac{222\cdot 3,5^2\cdot \pi^2}{2\pi}=\mbox{4271\,Hz}$$

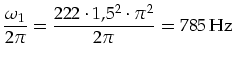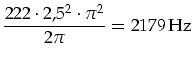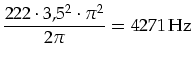Diese Eigenfrequenzen liegen deutlich über denen der Anregung. Das zum Vergleich im FE-System MARC/Mentat modellierte Modell ergibt dieselben Eigenfrequenzen. Die Modellierung ist mithin, zumindest wenn man die Dichte korrekt für die gewählten Einheiten einsetzt, verläßlich. Hier werden die Distanzen in mm und die Kräfte in N modelliert, die elastischen Werkstoffdaten sind in MPa=N/mm$^2$ angegeben, die Dichte beträgt dann $1,925\cdot 10^{-8}$.

Nun wird mit MARC/Mentat eine Glühwendel (OSRAM) modelliert und einige Varianten gerechnet. Der Faden wird in drei unterschiedliche Temperaturzonen aufgeteilt (vgl. Bild 3.13, oben links), für die Temperaturen angenommen werden und für diese Temperaturen werden die entsprechenden Werkstoffwerte eingesetzt.

A:

Beidseitig feste Einspannung, Werkstoffkennwerte nach Formel (3.38) und (3.39) für drei Zonen mit 0$^{\circ}$C, 1600$^{\circ}$C und 2300$^{\circ}$C.

B:

Wie A, zusätzlich wird in den Einspannungen wird die Rotation um die $y$-Achse zugelassen

C:

Wie B, zusätzlich wird in den Einspannungen wird die Rotation um die $z$-Achse zugelassen

D:

Wie C, zusätzlich wird in einer Einspannungen wird die Verschiebung in der $x$-Achse zugelassen

E1:

Der E-Modul im Bereich mit Raumtemperatur wird auf 300GPa reduziert

E2:

Wie E1, zusätzlich wird der E-Modul im Bereich mit 2300$^{\circ}$C auf 200GPa reduziert.

Es werden die ersten elf Eigenformen und -frequenzen berechnet. Siehe hierzu Tabelle 3.9 für die Frequenzen und Bild 3.13 für die Formen.

Tabelle 3.9: Eigenfrequenzen und Modellabhängigkeit

$i$	Grundmodell	Varianten (Angabe in Hz)
	A	B	C	D	E1	E1
1	3795	833	833	-0,13	3447	3305
2	3798	3798	834	2017	3449	3308
3	8644	5458	5457	2019	8150	7292
4	8648	8648	5469	6899	8155	7293
5	14130	14130		7113	13810	12180
6	14860	14760		7390
7	17990	15460
8	18000	17990
9	28370	28360
10	29530	28480
11	31500	29850

Es sind nicht alle Eigenfrequenzen aufgeführt. Ein relativ starker Eingriff in den E-Modul verschiebt die Eigenfrequenz nur unwesentlich. Lediglich die Freigabe der Rotationsmöglichkeit in den Einspannungen fügt eine weitere, relativ tiefe Frequenz und Form hinzu, die aber real nicht vorliegt, da die eingequetschte Einspannung dies nicht zuläßt.

Bild 3.13: Modellierung und Eigenformen (1, 3, 5, 6, 8, 9, 10, 11) eines Glühfadens (Rechenvariante A, Verschiebung nicht maßstäblich)

Diese Eigenfrequenzen liegen nicht im Bereich der Anregung. Daß einige Frequenzen und Formen so dicht beieinander liegen ist u.a. damit zu erklären, daß die Übergänge der Wendel auf den axialen Draht auf beiden Seiten freihand modelliert werden und leicht unterschiedlich sind.

Weitere Schwingungsformen könnten durch die elektrodynamischen Kräfte des Wechselstromes in den einzelnen Windungen auftreten. Dies dürften Transversalschwingungen sein, die aber erst ab der 6. Eigenfrequenz mit ca. 14kHz auftreten. Solch hohe Frequenzen erzeugen die meist verwendeten Generatoren normalerweise nicht.

Betrachtet man die errechneten Werte, so liegt maximal die niedrigste Eigenfrequenz im Bereich der Testfrequenzen nach DIN, nach ISO sogar keine. Hingegen sind die gemessenen Anregungen eher im Bereich der ISO oder der niedrigen nach DIN zu finden. Hier liegt eine Zwangserregung und keine Eigenschwingung vor. Der Frequenzbereich der ISO stimmt eher mit dem realen Problem überein. Die ISO ist der DIN vorzuziehen.