Fadengeometrie und -probleme

Der folgende Abschnitt ist ausgehend von den Beobachtungen mit sich kontaktierenden Windungen und partiellen Kurzschlüssen zu betrachten.

Nach ISO [ISO6742/1] sind die Bedingungen für den Schwingungstest von Fahrradbeleuchtung mit $12,5\pm0,8\bar{3}$Hz und einer Amplitude von 3mm anzusetzen. Dabei ist der Weg-Zeit-Verlauf kein Sinus sondern ein linearer Hub über ca. 0,069s mit einem folgenden federunterstützten Fall über ca. 0,011s. Der Prüfstand ist zu ungenau beschrieben, als daß man die Beschleunigungen ausrechnen oder den Prüfstand nachbauen könnte.

Die Norm EN [DIN EN 60810] sieht ein Schmalbandrauschen im Bereich von 30... 1050Hz, Bandbreite 100Hz, Mittelfrequenzbereich 80...1000Hz, Durchlaufgeschwindigkeit 1 Oktave/min, Durchlaufzeit je voller Zyklus 7,3min über 20h vor. Dabei liegt ein Schaltzyklus von 20min ein und 10min aus vor. Die spektrale Beschleunigungsdichte soll bei der Standardprüfung 0,12$g^2$/Hz(=3,5 $g_{\mbox{\footnotesize eff}}$) zwischen 80 und 150Hz sowie 0,014$g^2$/Hz(=1,2 $g_{\mbox{\footnotesize eff}}$) zwischen 150 und 1000Hz betragen. Bei der verschärften Prüfung betragen die Beschleunigungsdichten 0,36 bzw. 0,09$g^2$/Hz (=6 bzw. 3 $g_{\mbox{\footnotesize eff}}$). Die Frequenzen und Beschleunigungen richten sich nach den bei Automobilen auftretenden aus, bei Fahrrädern liegen andere Bedingungen vor. Eric Groß gibt in [Gr96] für das Oberrohr bzw. den Vorbau Frequenzen von 18...27Hz mit quadratischen Effektivwerten der Beschleunigungen von 5...15 $(\mbox{m/s}^2)^2$ bei Kopfsteinpflasterüberfahrten an. Die Spitzenbeschleunigungen liegen bei 14...28$g$ (Angaben jeweils gefederte Gabel...Starrgabel) . Dies entspricht spektralen Beschleunigungsdichten von ca.

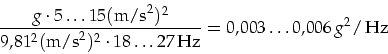$$\frac{g\cdot 5\ldots15 (\mbox{m/s}^2)^2}{9,81^2(\mbox{m/s}^2... ...ot 18\ldots 27\mbox{\,Hz}}=0,003\ldots 0,006\,g^2/\mbox{\,Hz}$$ (3.33)

Die Alterung soll vorher bei Prüfspannung über 30min erfolgen.^3.16

Nun ist zu klären, ob die Glühfäden im Bereich dieser Anregungen Eigenfrequenzen haben. Dafür sind Kenntnisse der Geometrie und des Werkstoffes notwendig.

An einigen Glühfäden werden mit einem Mikroskop die Fadengeometrien vermessen. Hierbei wird folgende Nomenklatur verwendet: Drahtdurchmesser $d$, Windungssteigung $D$, Windungszahl Einfachwendel bzw. Doppelwendel $i$, Außendurchmesser Windung $D$, Außendurchmesser Doppelwindung $D_1$, Steigung Doppelwendel $P_1$, Abstand Einspannung bis erste Windung $l$ und der rechnerischen Fadenlänge $L$. Wobei $L$ für Einfachwendeln mit

$$L=2 l+i(\pi (D-d)+0.2 P)$$ (3.34)

und für Doppelwendeln mit

$$L=[2l+i(\pi(D_1-d)+0.2 P_1)](\frac{\pi (D-d)}{P}+0.2)$$ (3.35)

abgeschätzt werden kann. Aus dem Widerstand der Lampe (gemessen mit dem HP in Vierleitermethode), dem spez. Widerstand von Wolfram bei Raumtemperatur (RT) $\varrho_{20\,^{\circ}\mbox{\footnotesize {C}}}=55$nm und dem Widerstand bei 1mA kann auf

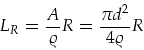$$L_R =\frac{A}{\varrho}R=\frac{\pi d^2}{4 \varrho}R$$ (3.36)

berechnet werden. Dabei werden Übergangswiderstände und die Zuleitung sowie eine Temperaturerhöhung durch den Meßstrom und dessen Einfluß auf $\varrho=f(\vartheta)$ vernachlässigt.

Tabelle 3.8: Fadengeometrien (Maße in mm)

Typ	Herst.	d	P	i	D	D_1	P_1	l	L	R	L_R
HS3	OSRAM	0,04	0,07	17	0,25	-	-	0,9...1	13,4	1,04	23
	OSRAM (1999)	0,04	0,065	22
	Tungsram	0,04	0,085	25	0,22	-	-	0,63...1,25	16,6
	Philips HMP08L	0,04	0,055	23		-	-	1,3
6V/3W	Philips HPR64	0,04	0,06	19	0,3	-	-	1,4	18,5	0,99	22
HS4	Philips HPR74	0,03	0,06	5	0,13	0,55	0,43	2	68,4	2,09	27
	Philips HPR78	0,06	0,11	16	0,37	-	-	2,3	26,6	0,47	24

Die Abweichungen zwischen $L$ und $L_R$ sind inakzeptabel groß. Hier scheint das Meßverfahren über den Widerstand nicht zulässig zu sein, da die Einflüsse der Übergangswiderstände und der Fadenhalter (Niro?) anscheinend zu groß sind. Hinzu kommt, daß gerade bei den HPR74 eingeschobene Stützdrähte sowohl stark von der Länge und Position her tolerieren und dadurch auch den Widerstand im Kaltbetrieb verfälschen.

Der Drahtdurchmesser liegt je nach Hersteller, soweit Daten verfügbar, bei:

Wolfram-Industrie:

(www.wolfram-industrie.com) 0,1, 0,2, 0,3 ...1,00, 1,2, 1,4...2mm

Midwest Tungsten Service:

(www.tungsten.com) 0,0127, 0,0254, 0,0508, 0,0762, 0,1016, 0,127, 0,1524, 0,1778, 0,2032, 0,2286, 0,254, 0,2794, 0,3048, 0,3302, 0,3556, 0,381, 0,4064, 0,4318, 0,4572, 0,4826, 0,508, 0,635, 0,762, 1,016, 1,143, 1,27, 1,524mm.^3.17

Goodfellows:

(www.goodfellows.com) 0,1, 0,125, 0,25, 0,5mm.

Tungsten Manufacturing Limited:

(www.tungsten.co.uk) 0,1...1mm.

OSRAM-Silvania:

Gibt den Drahtdurchmesser unter ca. 0,5 mm in $d$ [µm] über das Drahtgewicht $g$ [mg/200 mm] von 200 mm Draht an und bezieht sich dabei auf eine Dichte von 19,35g/cm$^3$. Minimaler Drahtdurchmesser sind 8µm.

$$d=18,1383\sqrt{g}$$ (3.37)

Die Drahtdurchmesser gehen von 615,5 mg/200mm jeweils in 0,5%-Schritten (Nennraster) mit einem Zwischenraster von 0,25%-Schritten bis auf 1mg/200mm runter. Genaueres hierzu in [OSRAMWolfram].

Hier sind nicht alle Drahtdurchmesser interessant. Jeder Hersteller hat seine eigenen Legierungen. Interessanterweise geben sich die wenigsten anscheinend mit den Drahtdurchmessern für Glühlampen ab.