Leistungsabschätzung für Laufräder

Durch die Luftströmung am Fahrradlaufrad wird eine Verlustleistung $P$ erzeugt. Hier werden ein paar Vereinfachungen getroffen:

• das Laufrad sei ein Scheibenrad

• das Laufrad drehe sich ohne Relativbewgung zum Boden

• Strömungsbeeinflussung durch Rahmen und Fahrer sei nicht gegeben

Dies führt dazu, daß die Leistung in der Praxis höher als hier berechnet sein sollte.

Als Eingangsdaten stehen folgende Randbedingungen zur Verfügung:

• Laufradumfang für 622er $U_{622}=2,07$ m, für 406er $U_{406}=1,47$ m.

• Fahrradgeschwindigkeit $v=30$ km/h

• Luftdruck $p_L=1,028$ bar

• Lufttemperatur $\vartheta_L=23$ $^{\circ}$C

Die Leistung $P$ ist

$$P=M \omega$$ (25)

Nach [1] B53 ist:

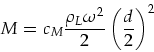$$M =c_M\frac{\rho_L \omega^2}{2}\left(\frac{d}{2}\right)^2\\$$ (26)

wobei

$$\omega = 2 \pi \frac{v}{U}$$ (27)

$$d = \frac{U}{\pi}$$ (28)

$$\rho_L = \frac{p_L}{R T_L}$$ (29)

$$T_L = \vartheta_L+273,15$$ (30)

mit dem Laufradduchmesser $d$ und der allgem. Gaskonstante $R=287$ J/(kg K).

Die Reynoldszahl²⁰ ist allgemein:

$$\mbox{Re}=\frac{v l}{\nu}$$ (31)

mit der Strömungsgeschwindigkeit $v$, der umströmten Länge $l$ und der Viskosität des Strömungsmediums $\nu$. Für rotierende Scheiben ist Re

$$\mbox{Re}=\frac{\omega d^2}{2 \nu}$$ (32)

mit der kinematischen Zähigkeit des Mediums $\nu$, für Luft bei 23 $^{\circ}$C ist $\nu\approx 15,9\cdot10^-6$ m$^2$/s.

Daraus folgt die Laufradleistung

$$P = c_M \frac{p_L}{2 R T_L}\left(\frac{2 \pi v}{U}\right)^3\left(\frac{U}{2 \pi}\right)^2$$

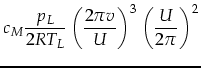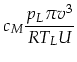$$= c_M \frac{p_L \pi v^3}{R T_L U}$$ (33)

Folglich haben größere Laufräder ein kleinere aerodynamische Verlustleistung, wenn $c_M$ nicht mit der Laufradgröße zu stark ansteigt.

Der Widerstandsbeiwert ist vom Einbau und der Reynoldszahl abhängig. Ist $\mbox{Re}>3\cdot10^5$, so ist die Strömung turbulent und es ist $c_{M_t}$ zu verwenden. Bei $\mbox{Re}<3\cdot10^5$ sonst ist die Stömung laminar und es ist $c_{M_l}$ zu verwenden.

$$c_{M_l} = \frac{5,2}{\sqrt{\mbox{Re}}}$$ (34)

$$c_{M_t} = \frac{0,168}{\sqrt[5]{\mbox{Re}}}$$ (35)

Läuft die Scheibe in einem Gehäuse mit dem Abstand $s$ zwischen Scheibe und Gehäusewandung, so gelten für $c_M$ die Gleichungen (36)-(38).

$$c_{M_{G, Re<3\cdot 10^5}} = \frac{2 \pi d}{s \mbox{Re}}$$ (36)

$$c_{M_{G, 3\cdot 10^3<Re<6\cdot 10^5}} = \frac{3,78}{\sqrt{\mbox{Re}}}$$ (37)

$$c_{M_{G, 6\cdot 10^5<Re}} = \frac{0,0714}{\sqrt[5]{\mbox{Re}}}$$ (38)

Die sich in der Berechnungen ergebenden Werte sind in Tabelle 14 aufgeführt.

Tabelle 14: Berechnungsgrößen für Scheibenräder

Größe	406		622
	laminar	turbulent	laminar	turbulent
$U$	1,47		2,07
$d$	0,468		0,659
$\omega$	35,62		24,54
Re	245327		341420
$c_{M_{frei}}$	0,0105	0,014	0,0089	0,0134
$P_{frei}$	15,7	21,0	9,5	14,4
$c_{M_{geh\uml {a}use}}$	-	0,0064	-	0,0065
$P_{geh\uml {a}use}$	-	11,65	-	6,9

Da davon auszugehen ist, daß Fahrradlaufräder turbulent umströmt sind (siehe alleine die Größe der Reynoldszahl), könnte durch eine Einkastung der Laufräder die Leistung ungefähr um ca. 50 % gesenkt werden. Dies ist die Leistung der rotierenden Scheibe, davon unbeeinflußt sind Strömungsverluste durch Verwirbelung restlichen, nachfolgenden Fahrradteilen. Eine ,,Milchmädchenrechnung`` ergäbe dann, 150 W Antriebsleistung vorausgesetzt, bei 15 W mehr zur Verfügung stehender Leistung (an den Laufrädern eingespart) eine potentielle Geschwindigkeitssteigerung von ca. 2-3 %.²¹