Keine Berücksichtigung von Verlusten

Ein einfache Bilanzierung des Systemes liefert die folgende Lösung. Dabei werden jegliche Verluste vernachlässigt. Der Höhenunterschied von ca. 35 m entspricht dem, der unten beschriebenen, Kuhtrift. Bei dieser Betrachtung wird angenommen, daß der Fahrer nicht mittritt. Im Programm dient es zum Abschätzen von $v_{max}$ .

$\displaystyle V_2+U_2$	$\textstyle =$	$\displaystyle V_1+U_1$	(5)
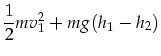$\displaystyle \frac{1}{2}m v_2^2$	$\textstyle =$	$\displaystyle \frac{1}{2}m v_1^2+m g (h_1 - h_2)$
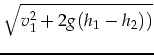$\displaystyle v_2$	$\textstyle =$	$\displaystyle \sqrt{v_1^2+2 g (h_1 - h_2))}$	(6)
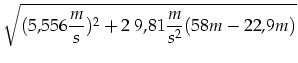$\displaystyle v_2$	$\textstyle =$	$\displaystyle \sqrt{(5,556\frac{m}{s})^2+2\ 9,81\frac{m}{s^2} (58m-22,9m)}$
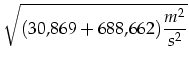$\displaystyle v_2$	$\textstyle =$	$\displaystyle \sqrt{(30,869+688,662) \frac{m^2}{s^2}}$
$\displaystyle v_2$	$\textstyle =$	$\displaystyle 26,82~m/s = 96,95~km/h$

Diese Geschwindigkeit wird sich nie einstellen, da beim Rollen Verluste auftreten, die das Fahrrad abbremsen. So wird die zur Verfügung gestellte Höhenenergie nicht komplett in kinetische Energie, und damit Geschwindigkeit, umgewandelt.

Der Beitrag von

mit $\sqrt{30,869\mbox{ m}^2/\mbox{s}^2}=5,56$ m/s verschwindet gegenüber $\sqrt{688,662\mbox{ m}^2/\mbox{s}^2}=26,24$ m/s. Oder anders: Ein Abweichung bei

von 10 % oder $\pm 2$ km/h wirkt sich mit einem Fehler in der Endgeschwindigkeit 0,4 % aus. Die Startgeschwindigkeit ist die, für die Kuhtrift standardisierte von 20 km/h.