Spannungsüberhöhung

Der Ansatz von Wullkopf deckt nicht ab, daß das System durch einen externen Kondensator mit Spannungsüberhöhungen am Widerstand reagieren kann. Bei einer geeigneten Abstimmung wird bei einer bestimmten Frequenz, mithin Geschwindigkeit, eine Spannungsüberhöhung erreicht.

Im folgenden der Gedankengang von Ralf Kusmierz. Eine Veröffentlichung ist in [KusPV4] zu finden. Hier hat Ralf eine ausformuliertere Fassung zur Verfügung gestellt. Auf diesen Ansatz hatte Ralf ein Patent (P3345210) [KusPV5]. Ralf ging es nicht um die Leistungsmaximierung sondern um ein möglichst frühes Bereitstellen der elektrischen Leistung, damit auch bei niedrigen Geschwindigkeiten viel Licht vorhanden ist.

Das Schaltbild und das Ersatzschaltbild des Systemes ist im Bild 2.2 wiedergegeben.

**Bild 2.2:** Schaltbild und Ersatzschaltbild beim Serienkondensator
$\begin{figure}\centering \centering \includegraphics[width=9cm]{bilder/ErsatzKuszmi1}\end{figure}$

Die Kreisfrequenz $\omega$ , Leerlaufspannung

, wirksame Impedanz

des Kreises sind

$\displaystyle \omega$	$\textstyle =$	$\displaystyle 2 \pi f\sim v$	(2.2)
$\displaystyle U_0$	$\textstyle =$	$\displaystyle \omega E$	(2.3)
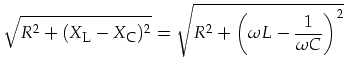$\displaystyle Z$	$\textstyle =$	$\displaystyle \sqrt{R^2+(X_{\mbox{\footnotesize L}}-X_{\mbox{\footnotesize C}})^2}=\sqrt{R^2+\left(\omega L-\frac{1}{\omega C}\right)^2}$	(2.4)
$\displaystyle R$	$\textstyle =$	$\displaystyle R_{\mbox{\footnotesize a}}+R_{\mbox{\footnotesize i}}$	(2.5)

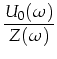$\displaystyle I(\omega)$	$\textstyle =$	$\displaystyle \frac{U_0(\omega)}{Z(\omega)}$	(2.6)
$\displaystyle \lim_{\omega\rightarrow\infty} I(\omega)$	$\textstyle =$	$\displaystyle \frac{E}{j L}$	(2.7)
$\displaystyle P_{\mbox{\footnotesize a}}(\omega)$	$\textstyle =$	$\displaystyle \vert I\vert^2R_{\mbox{\footnotesize a}}$	(2.8)

Zweckmäßigerweise normiert man $P_{\mbox{\footnotesize a}}(\omega)$ für hohe Geschwindigkeiten und erhält

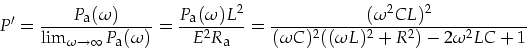$\begin{displaymath} P'=\frac{P_{\mbox{\footnotesize a}}(\omega)}{\lim_{\omega\ri... ...(\omega^2CL)^2}{(\omega C)^2 ((\omega L)^2+R^2)-2\omega^2LC+1} \end{displaymath}$

(2.9)

$\displaystyle \omega$	$\textstyle =$	$\displaystyle \omega'\frac{R}{L}$	(2.10)
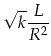$\displaystyle C$	$\textstyle =$	$\displaystyle \sqrt{k}\frac{L}{R^2}$	(2.11)

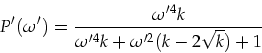$\begin{displaymath} P'(\omega')=\frac{\omega'^4k}{\omega'^4k+\omega'^2(k-2\sqrt{k})+1} \end{displaymath}$

(2.12)

Dieser Ausdruck hängt nur noch von dem Parameter

, der die Größe der Kapazität beschreibt, und dem geschwindigkeitsproportionalen $\omega'$ ab. Wird der Ausdruck $P'(\omega)$ für verschiedene

gezeichnet, dann ist die Wirkung verschiedener Kapazitäten gut zu erkennen (vgl. Bild 2.3).

**Bild 2.3:** Auswirkung von k= und o= $\omega'$ auf P'=
$\begin{figure}\centering \includegraphics[width=10cm]{bilder/kKuszmi} \end{figure}$

Für $k\rightarrow\infty$ ergibt sich der Fall ohne Kondensator $P'=\omega'^2/(\omega'^2+1)$ . Die Differenz zwischen Kondensator und nicht Kondensator ist in Bild 2.4 wiedergegeben.

**Bild 2.4:** Gewinn durch den Kondensator
$\begin{figure}\centering \includegraphics[width=8cm]{bilder/gKuszmi} \end{figure}$

$\begin{displaymath} C=\sqrt{k}\frac{L}{(R_{\mbox{\footnotesize a}}+R_{\mbox{\footnotesize i}})^2} \end{displaymath}$

(2.13)

Der Kondensator darf, da Wechselspannung, kein normaler Elektrolytkondensator (Elko) sein! Mit bipolaren Elkos (Tonfrequenz-Elkos) könnte es mal probiert werden. Oder mit zwei antiseriellen Elkos mit doppelter Kapazität oder..., es gibt halt viele Möglichkeiten.

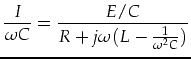$\displaystyle U_{\mbox{\footnotesize C}}$	$\textstyle =$	$\displaystyle \frac{I}{\omega C}=\frac{E/C}{R+j\omega(L-\frac{1}{\omega^2C})}$	(2.14)
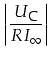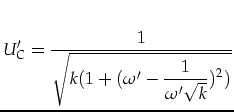$\displaystyle \left\vert\frac{U_{\mbox{\footnotesize C}}}{RI_{\infty}}\right\vert$	$\textstyle =$	$\displaystyle U'_C=\frac{1}{\sqrt{k(1+(\omega'-\displaystyle \frac{1}{\omega'\sqrt{k}})^2)}}$	(2.15)
$\displaystyle \hat{U}'_{\mbox{\footnotesize C}}$	$\textstyle =$	$\displaystyle \frac{1}{\sqrt{k}}$	(2.16)

Als kritische Betrachtung des Ansatzes mag folgendes gelten. Der elektrische Wirkungsgrad $\eta_{\mbox{\footnotesize el}}$ ergibt sich

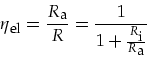$\begin{displaymath} \eta_{\mbox{\footnotesize el}}=\frac{R_{\mbox{\footnotesize ... ...\frac{R_{\mbox{\footnotesize i}}}{R_{\mbox{\footnotesize a}}}} \end{displaymath}$

(2.17)

Der Lastwiderstand ist durch gesetzliche Vorgaben festgelegt. Der elektrische Wirkungsgrad kann nur durch den Innenwiderstand beeinflußt werden. Je kleiner der Innenwiderstand, desto besser der elektrische Wirkungsgrad. Bei den typischen Fahrraddynamos liegt der elektrische Wirkungsgrad bei 70-85%.

Das mag ersteinmal reichen. Vielen Dank an Ralf für seine Informationen und Diskussionsbereitschaft, diese Erweiterung ist durch sein Dazutun gewachsen.^2.4