Widerstand etc.

LEDs haben keinen linearen, geschweige denn einen konstanten Widerstand. Für theoretische Überlegungen ist ein funktionaler Zusammenhang wünschenswert. Leider streuen LEDs stark in ihrem elektrischen Verhalten (vgl. Bild 3.45) und damit auch die Parameter der Approximation. Hier wird eine mittlere Kurve von zwölf getesteten Cree XR7090-WT-U1 (XR-E) verwendet.

Grundlage ist die für ,, normale`` Dioden gut zutreffende Exponentialfunktion für

, der für LEDs ein Serienwiderstand (

) hinzugefügt werden sollte.

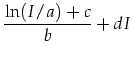$\displaystyle U(I)$	$\textstyle =$	$\displaystyle \frac{\ln(I/a)+c}{b}+dI$	(3.64)
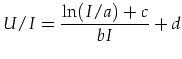$\displaystyle R(I)$	$\textstyle =$	$\displaystyle U/I=\frac{\ln(I/a)+c}{bI}+d$	(3.65)
$\displaystyle I(U)$	$\textstyle =$		(3.66)

Mit $a=3,03178\cdot10^{-19}$ ,

und

für

in Volt,

in Ampere und

in Ohm ist die Annäherung schon recht gut (vgl. Bild 3.50)

**Bild 3.50:** Spannung über Strom einer XR7090-WT-U1
$\begin{figure}\centering \includegraphics[width=6cm]{Meszwerte/LEDs/Cree/exponentialfit} \end{figure}$

$\displaystyle I_{\mbox{\footnotesize Cree exp}}$

$\textstyle =$

(3.67)

Damit ist dann über

der Einsatz in Gl. 2.1 möglich. Wobei noch der Gleichrichter etc. zu berücksichtigen wäre. Siehe hierzu Seite

In technisch interessanten begrenztem Bereich zwischen ca. 0,001...0,8A kann auch folgender Zusammenhang verwendet werden:

$\begin{displaymath} R(I) =3,6 I^{-0,94} \end{displaymath}$

(3.68)

Die Parameter sind passen bei je vier Luxeon Rebel, vier Seoul P4 und zehn Cree XR-E hinreichend gut (vgl. Bild 3.51).

**Bild 3.51:** Widerstand von LEDs als Funktion des Stromes
$\begin{figure}\centering \includegraphics[height=10cm]{Meszwerte/LEDs/Seoul/RvonI} \end{figure}$

Auch die die Helligkeit bzw. der Lichtstrom kann über die Spannung bzw. Strom angegeben werden. Jedoch bietet sich hier eher eine Bezug an, z.B. auf den bei 500mA. Dann Der Verlauf ist für 2007/2008 aktuelle LEDs Cree XR-E, Luxeon Rebel und Seoul P4 nahezu identisch (vgl. Bild 3.52).

$\begin{displaymath} \Phi(I)/\Phi(500\mbox{\,mA}) =-0,0012+2,56 I-0,883 I^2 \end{displaymath}$

(3.69)

Mit

in Volt,

in Ampere und $\Phi$ bezogen. Weitere Approximationen sind auf Seite F.9 in Bild F.9 aufgeführt.

**Bild 3.52:** Lichtstrom von LEDs als Funktion des Stromes (bezogen auf den bei 500 mA)
$\begin{figure}\centering \includegraphics[height=10cm]{Meszwerte/LEDs/Seoul/Phi_von_I_poly1} \end{figure}$

Mit diesen Formeln, denen aus Abschnitt 2.1 bzw. F.1, J und 3.8.8 sollte dann eine hinreichend genaue funktionale Beschreibung des Verhaltens der Lichtanlage gegeben sein.